
Masked Diffusion Models (MDM) have been a promising alternative to autoregressive models, with recent scaling-up efforts, e.g., LLaDA, Dream7B, Mercury, Gemini Diffusion. Despite these successes, they struggle to (1) model variable-length sequence distributions and (2) insert new tokens during generation.
FlexMDM addresses these issues: By baking in the ability to insert mask tokens, FlexMDM exhibits superior performance over masked diffusion in planning and reasoning tasks where length flexibility is crucial.
FlexMDM scales up to 8B parameters—we retrofit LLaDA, an 8B open-sourced pretrained MDM, and fine-tune it using 1000 H100 GPU hours. FlexMDM's ability to insert new tokens in arbitrary positions enables better reasoning capabilities on real-world reasoning tasks such as math (GSM8K) and code infilling (Humaneval-infill). Compared to MDM, FlexMDM achieves superior performance on math (GSM8K, 58%→67%) and code infilling (52%→65%)
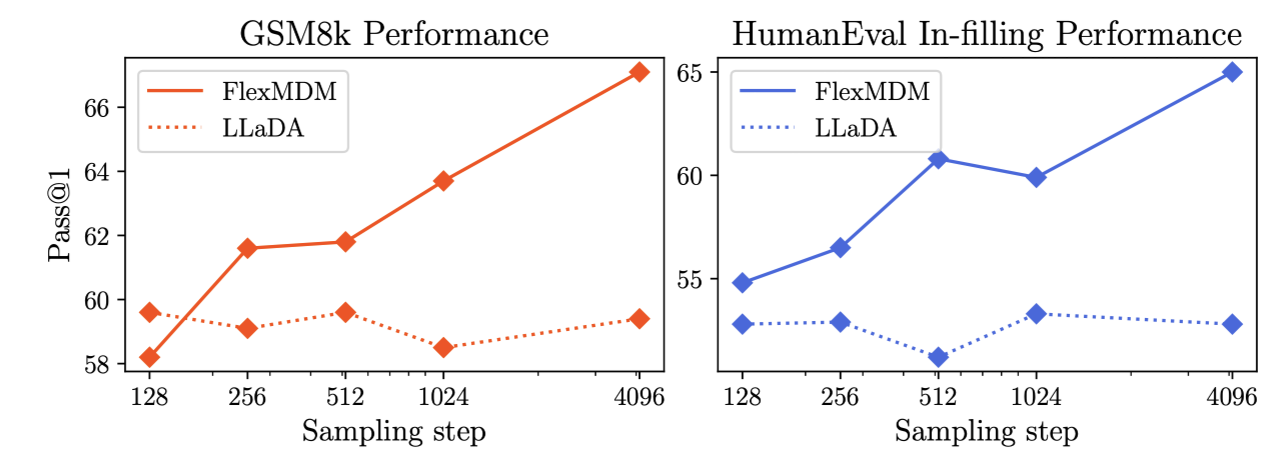
We retrofit an 8B parameter LLaDA model into FlexMDM using 1000 H100 GPU hours. By allowing the model to insert new tokens in arbitrary positions, FlexMDM exhibits better reasoning capabilities on real-world reasoning tasks such as coding and grade school mathematics.
| Difficulty | MDM | FlexMDM |
|---|---|---|
| Easy | 68.4% | 92.3% |
| Medium | 29.3% | 90.4% |
| Hard | 24.2% | 90.0% |
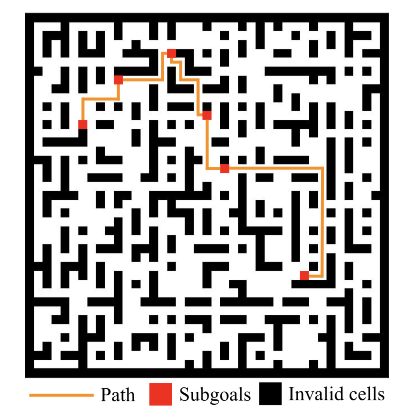
Trajectories in planning tasks are inherently variable-length. By allowing the model to insert new tokens in arbitrary positions, FlexMDM is able to generate more trajectories that pass through subgoals in a valid way.
The modeling of the method relies on joint interpolants, an extension of the stochastic interpolant. In essence, the interpolant framework facilitates the construction of generative models by defining a collection of time-indexed random variables that govern the marginal probability of the generation at time t and describe the mathematical quantities required for generation.
In the context of FlexMDM, we bridge between a point mass at an empty sequence and data distribution $p_1$. The intermediate distribution follows the distribution of $x_t$, which we define per dimension by sampling an insertion time $T_1$ and unmasking time $T_2$ :
$$ \quad T_2^i \sim \mathbf{1}_{\{t \ge T_1^i\}}\frac{\dot{\beta_t}}{1-\beta_{T_1}} \; dt, \quad x_t^i = \begin{cases} \text{(empty)}, & 0 < t < T_1^i \\ \mathbf{m}, & T_1^i \leq t < T_2^i \\ x_1^i, & T_2^i \leq t \leq 1 \end{cases} $$This is augmented by an auxiliary variable defined in a way that is coupled with $x_t$: $$ s_t \colon= \{i \in \{0,\dots,\mathrm{len}(x_1)-1\} \mid T_1^i \le t\}, $$ which is the set of indices that have been inserted by time $t$. Jointly with $x_t$, they characterize the quantities needed to define the inference procedure:
We outline two inference algorithms for FlexMDM: vanilla inference and adaptive inference.
Vanilla inference. We discretize the CTMC using trained neural networks $(f_\theta,g_\theta)$ with $\tau$-leaping. At each step, we simultaneously:
Adaptive inference. We can choose unmasking positions adaptively, prioritizing the most confident indices based on the model's unmasking posterior or semi-autoregressive rules. This substantially boosts performance.
Key Result: Any sampling scheme that (i) unmasks arbitrary subsets but draws tokens from the ground-truth unmasking posterior and (ii) applies insertion CTMC governed by the ground-truth rate matrix samples from the target distribution $p_1$.
Require: Learned functions ($f_{\theta}, g_{\theta}$)
Require: Discretization $0 = t_1 < \dots < t_N = 1$
Require: Insertion, Unmasking schedule $\alpha_t, \beta_t$
@article{kim2025any,
title={Any-Order Flexible Length Masked Diffusion},
author={Kim, Jaeyeon and Cheuk-Kit, Lee and Domingo-Enrich, Carles and Du, Yilun and Kakade, Sham and Ngotiaoco, Timothy and Chen, Sitan and Albergo, Michael},
journal={arXiv preprint arXiv:2509.01025},
year={2025}
}